
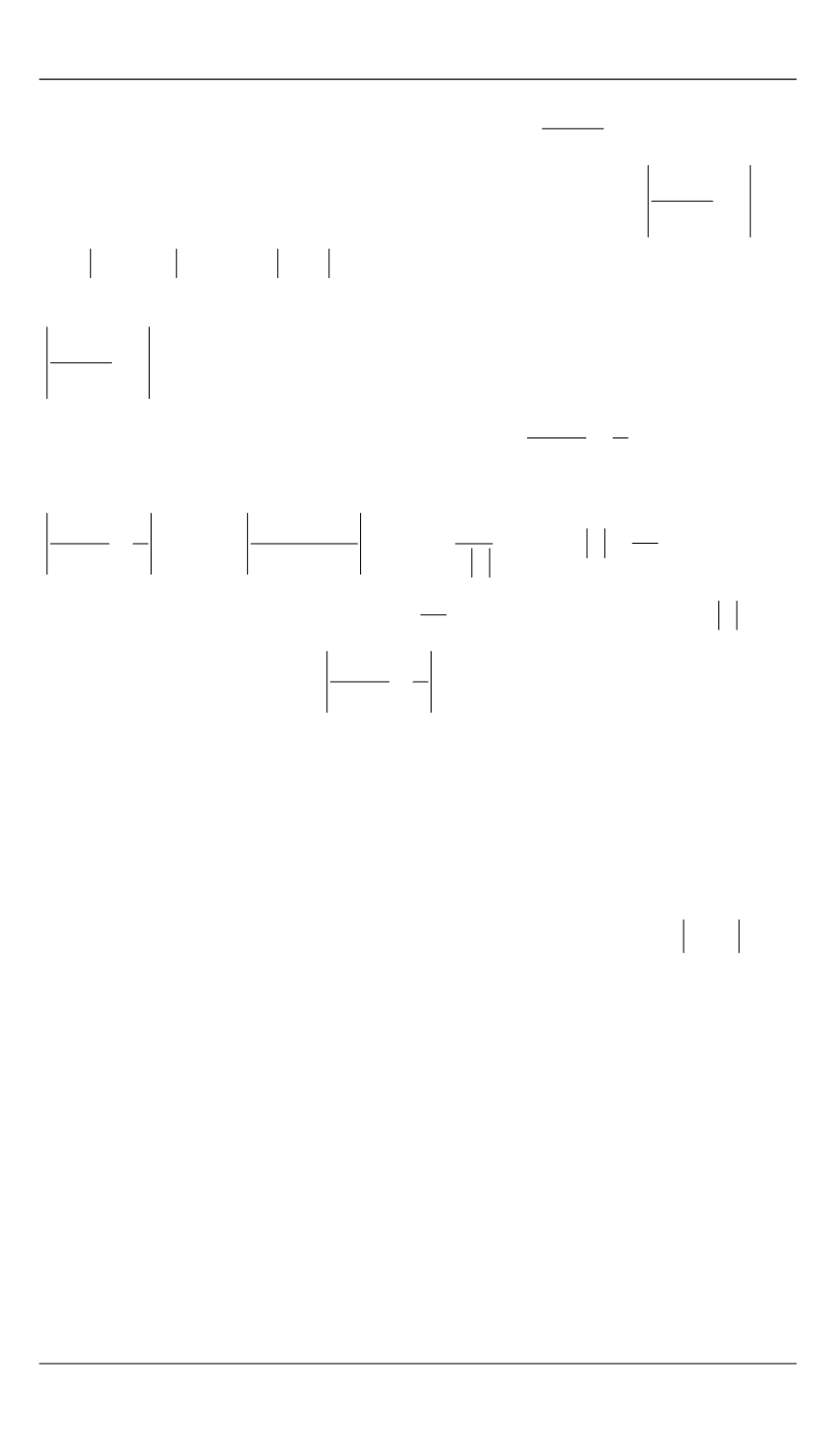
Методические аспекты подходов к преподаванию теории пределов функций
Гуманитарный вестник
# 5·2016 5
Задача 2.
Доказать по определению:
2
3 0
9
lim
6
3
x
x
x
→ +
− =
−
.
Возьмем произвольное
0
ε >
и найдем
( )
0
δ = δ ε >
:
2
9 6
3
x
x
− − 9 ε
−
⇔
3 6
x
+ − < ε
⇔
( )
3
x
− < ε = δ ε
. Таким образом, для
0
∀ε >
∃
( )
0
δ ε = ε >
такое, что для
: 3 3
x x
∀ < < + δ
выполняется неравенство
2
9 6
3
x
x
− − 9 ε
−
.
Задача 3.
Доказать по определению:
2 1 2
lim
3 3
x
x
x
→∞
+ =
.
Возьмем произвольное
0
ε >
и найдем
( )
0
M M
= ε >
:
2 1 2
3 3
x
x
+ − < ε
⇔
2 1 2
3
x
x
x
+ − < ε
⇔
1
3
x
< ε
⇔
( )
1
3
x
M
> = ε
ε
. Та-
ким образом, для
0
∀ε >
∃
1 0
3
M
= >
ε
такое, что для
:
x x M
∀ >
выполняется неравенство
2 1 2
3 3
x
x
+ − < ε
.
Приведем теоремы, которые послужат теоретическим обоснова-
нием при решении задач.
Теорема 1
(о единственности предела). Если предел функции в
точке существует, то он единствен.
Определение 12.
Функция
( )
y f x
=
называется
локально ограни-
ченной
, если она ограничена при
x a
→
: существует такое
0
c
>
и та-
кая
( )
U a
a
, что для всех
( )
x U a
∈
a
выполняется неравенство
( )
f x c
≤
.
Пример 1.
Функция
2
2
y x
= +
локально ограничена при
0
x
→
.
Теорема 2
(о локальной ограниченности функции, имеющей ко-
нечный предел). Если функция
( )
y f x
=
имеет конечный предел в
точке
x a
=
, то она локально ограничена.
Теорема 3
(о пределе промежуточной функции). Если существу-
ют конечный
( )
lim
x a
f x A
→
=
, конечный
( )
lim
x a
g x A
→
=
и такая
( )
U a
a
, что
для любых
( )
x U a
∈
a
выполняется неравенство
( ) ( )
( )
f x h x g x
≤ ≤
, то
существует конечный
( )
lim
x a
h x A
→
=
.


















