
Н.С. Васильев, В.И.
Громыко
10
2)
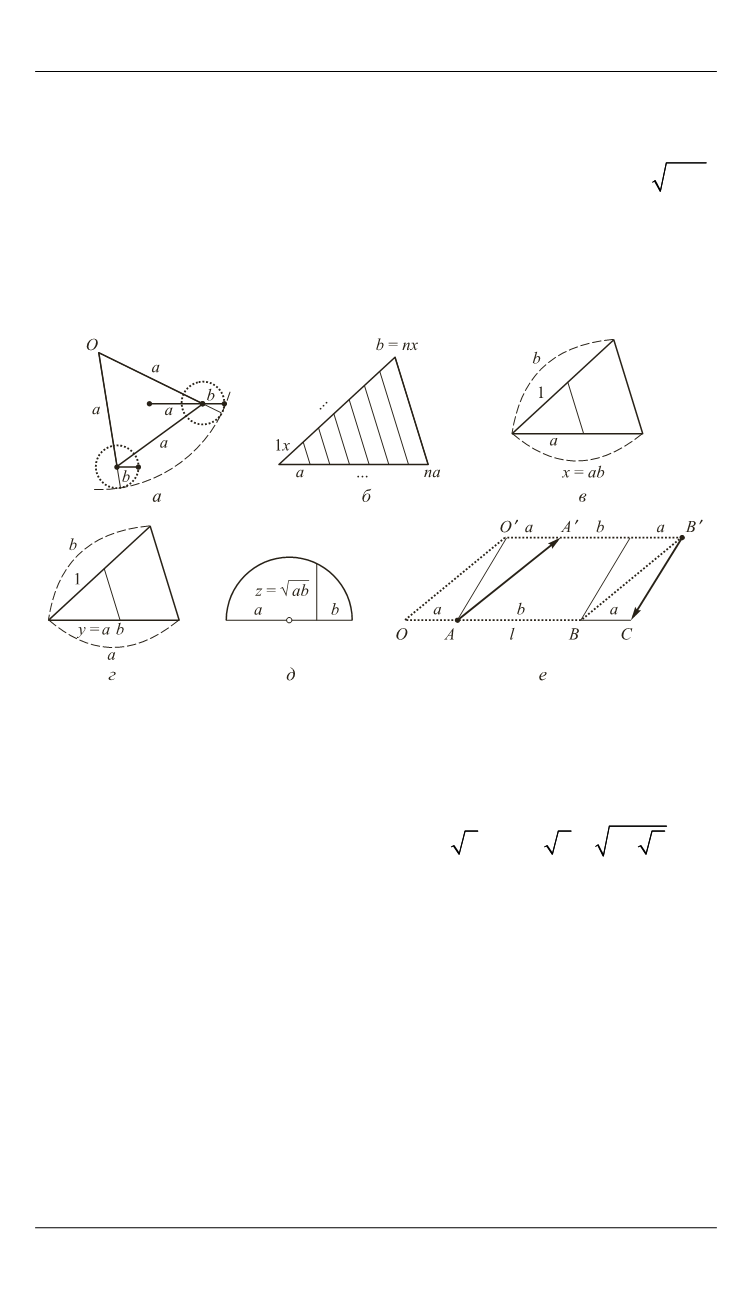
умея проводить параллельную прямую, можем поделить отре-
зок
b
на
n
равных частей (рис. 5,
б
);
3)
после расширения пропорции до несоизмеримых отрезков
(Евдокс, кн. 5) можем строить отрезки
x ab
,
/ и
( )
y a b z
ab
(рис. 5,
в
−
д
);
4)
в исчислении доказывается, что
(
) (
);
a b b a
O A A B
a b AB BC b a
(рис. 5,
е
).
Рис. 5.
Исчисление отрезков Гильберта применительно к планиметрии Евклида
Таким образом, множество вещественных чисел
Евклида
R
является
предельным расширением поля
Q
:
2
2 1 2
Q Q Q
Б. Исчисление отрезков Гильберта
это абстрактный тип дан-
ных, развернутый на аксиоматической базе свойств отношений ин-
цидентности, линейности (аксиома Паша), конгруэнтности, парал-
лельности (аксиома Евклида), архимедовости и линейной полноты
поля вещественных чисел. Геометрия строится моделированием воз-
можностей линейки и «распространением» конгруэнтных углов и от-
резков. Таким способом получают обоснование декартизации и ове-
ществление геометрии:
Гильберта
R
= поле, которое архимедово упоря-
дочено и максимально.
В связи с этим на вопрос о том, что такое
прямая на плоскости, не следует удивляться алгебраическому отве-
ту. Это — множество
( , )|
0 .
x y ax by c
/

















