М.Н. Захаров, П.А. Николаев
8
Достаточно часто используются минимизация издержек и ма-
тематическое ожидание от ущерба, вызванного простоем произ-
водства вследствие отсутствия материалов. В простейшем случае
приходим к оптимизационной задаче вида:
C x x x
P x x x C x x x
n
n
n
( , , , )
( , , , ) ( , , , ) min;
1 2
1 2
1 1 2
1
… + −
…
(
)
⋅
… →
P
(
x
1
,
x
2
, …,
x
n
)
≥
P
*
,
где
С
1
— сумма потерь, связанных с простоями производства.
Из практики проектирования логистических цепей извест-
но, что затраты на управление цепочкой поставок увеличиваются
ускоренными темпами при увеличении требований к уровню на-
дежности системы. В то же время при возрастании уровня надеж-
ности снижается ожидаемый ущерб от простоя производства
C
U
,
вычисляемый следующим образом:
C
P x x x C x x x
U
n
n
= −
…
(
)
⋅
…
1
1 2
1 1 2
( , , , ) ( , , , ).
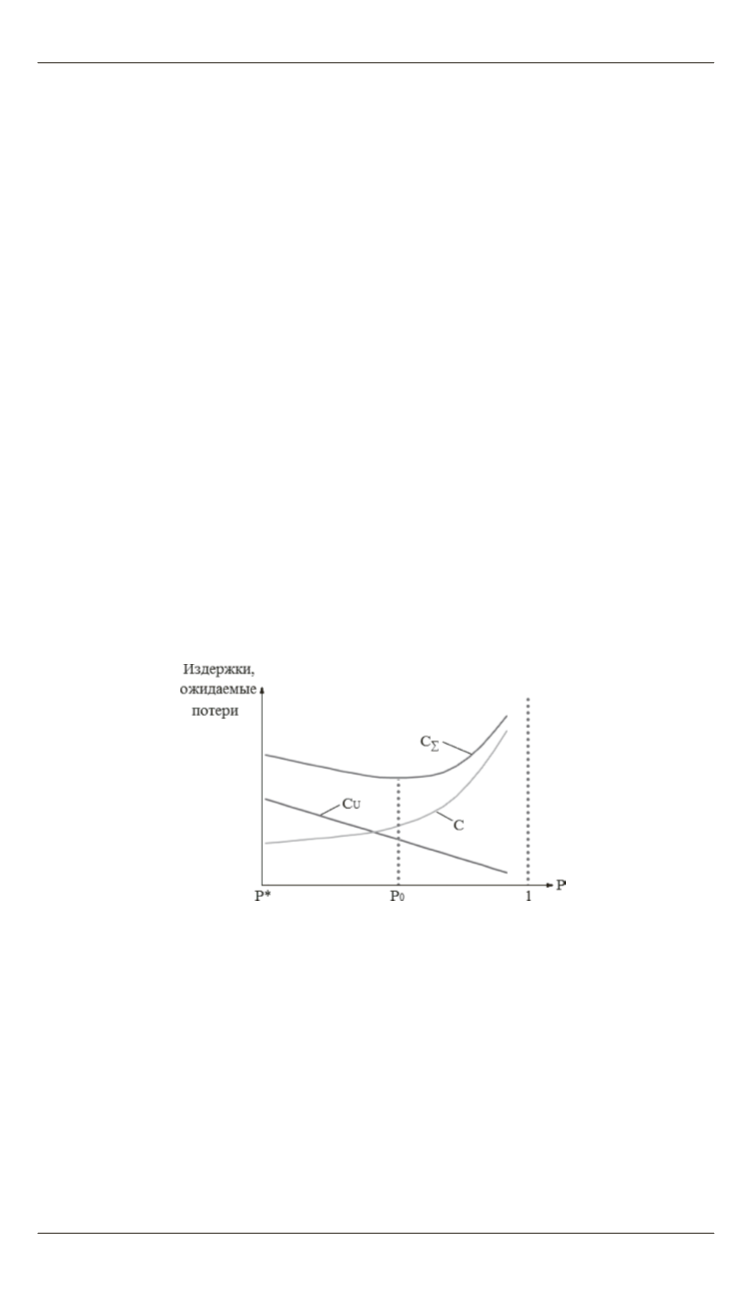
В этом случае оптимальным, с точки зрения экономической
обоснованности, будет такой уровень надежности
P
0
, при котором
сумма затрат по обеспечению этого уровня будет минимальна:
C
Σ
=
C
U
+
C
→
min.
Графически данная ситуация проиллюстрирована на рис. 3.
Рис. 3.
Минимизация суммарных ожидаемых затрат
В некоторых случаях рассмотренной оптимизационной зада-
чи не вводится ограничение по надежности. Например, для малых
и средних фирм издержки, связанные с отсутствием материалов,
сопоставимы с издержками на доставку и хранение. Но на пред-
приятиях тяжелого машиностроения, энергетики или оборонной
промышленности низкая надежность поставок способна вызвать
негативные эффекты, ущерб от которых ни в коем случае нель-
зя недооценивать. Поэтому при проектировании логистической
цепи для таких предприятий целесообразно вводить ограничение
по надежности.


